[컴퓨터구조] 수의 체계 / 2진수

● 수의 체계 ( Number Systems )

 

1) 10진수 (Decimal numbers)

2) 2진수 (Binary numbers)

3)N-digit decimal number 

  ○ How many values?  10^N

  ○ Range?  0 ~ 10^N -1

  ○ usally Hexadecimal Numbers (16진수) : Shorthand for Binary

 

 

 ● 2 진법 표현

일상 생활에서는 10진법을 사용하지만 컴퓨터는 2진법으로 이용해 작동이 되기 때문에 

사용하는 숫자를 2진법으로 표현을 하려 했다.

 

1) Signed Binary Numbers

   맨 왼쪽의 비트를 부호 비트하여 음/양수를 구분하는 방법 

 

▶문제점

1000  (-0)

0000  (+0)

± 0  0은 1개 이지만 표현 방식이 2개가 생기는 문제 

 

2) One`s Complement Numbers (1의 보수)

모든 비트의 값을 반대로 뒤집는 형식

예를 들면 양수 5를 2진수로 0101 표현 음수 5를 표현할 때  모든 값을 not으로 표현 1010 

 1010 을 -5로 표현하는 방식

▶문제점

0000  (+0)

1111  (-0)

기존과 동일하게 0이 2개의 표현 방식으로 나타남

 

3) Two’s Complement Numbers (2의 보수)

 - 전환 방법
    ① 1의 보수로 변경(모든 비트를 반전)
    ② 1을 더한다.

- 예시

+7 : 0111

 ① : 1000

 ② : 1001  -7 을 표현

2의 보수로 표현하게 되면 -0으로 표현되는 부분이 없어지면서 4bit기준으로 -8~+7 16가지를 모두 나타낼 수 있다.

 

 

 ● 2 진법의 덧셈

 

일반적으로 10진법에서 덧셈을 하게되면 10넘어가는 경우
Carries (캐리)된다고 표현한다. 

 

 

 

 

 

---

 

2진법에서는 2가 넘어가는 경우를 Carries (캐리)되다고 하고 덧셈을 하면 됩니다.

 

 

 

 

 

 

 

 ● 오버플로우(Overflow)

 

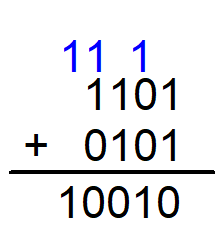
예를들어  1101 + 0101을 덧셈을 하면 10010 이 나온다.

만약에 4bit 연산을 하는 장치라 저장을 할 수 있는 공간이 4bit 밖에 없다면

10010 실제로 저장될 때 0010로 저장이되면서 다른 값이 되는 현상이 나타난다.

이 부분을 Overflow가 발생되었다고 표현한다.

 

 

 

오버플로우 판단

 

4

3

2

1

3번 부분을 C1 4번 부분을 C2 일 때 해당 부분에 캐리가 발생되면 1 발생되지 않으면 0 

 

1) 0001 + 1111 ( 1 + -1 )  

0001

1111

-------

10000     => C1 : 1 / C2 : 1  ≫ 오버플로우 X

2) 0111 + 0001 (  7 + 1 )

0111  

0001

-------

1000      => C1 : 1 / C2 : 0  ≫ 오버플로우 O

3) 0001 + 0001 ( 1 + 1 )

0001 

0001

-------

0020      => C1 : 0 / C2 : 0  ≫ 오버플로우 X

4) 1000 + 1000 ( -8 + -8 )

1000

1000

-------

10000    => C1 : 0 / C2 : 1  ≫ 오버플로우 O

 

carry_in != carry_out

 

 

 ● 비트 확장(Increasing Bit Width)

언젠가 추가하겠지?!